Partition of an interval

In mathematics, a partition, P of an interval [a, b] on the real line is a finite sequence of the form

a = x₀ < x₁ < x₂ < ... < x_n = b.

Such partitions are used in the theory of the Riemann integral, the Riemann–Stieltjes integral and the regulated integral. Another partition of the given interval, Q, is defined as a refinement of the partition, P, when it contains all the points of P and possibly some other points as well; the partition Q is said to be “finer” than P. Given two partitions, P and Q, one can always form their common refinement, denoted P ∨ Q, which consists of all the points of P and Q, re-numbered in order.

The norm (or mesh) of the partition

x₀ < x₁ < x₂ < ... < x_n

is the length of the longest of these subintervals, that is

max{ |x_i − x_i−1| : i = 1, ..., n }.

As finer partitions of a given interval are considered, their mesh approaches zero and the Riemann sum based on a given partition approaches the Riemann integral.

A tagged partition is a partition of a given interval together with a finite sequence of numbers t₀, ..., t_n−1 subject to the conditions that for each i,

x_i ≤ t_i ≤ x_i+1.

In other words, a tagged partition is a partition together with a distinguished point of every subinterval: its mesh is defined in the same way as for an ordinary partition. It is possible to define a partial order on the set of all tagged partitions by saying that one tagged partition is bigger than another if the bigger one is a refinement of the smaller one.

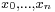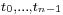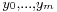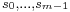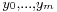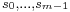Suppose that $\scriptstyle x_0,\ldots,x_n$ together with $\scriptstyle t_0,\ldots,t_{n-1}$ is a tagged partition of $[a, b]$ , and that $\scriptstyle y_0,\ldots,y_m$ together with $\scriptstyle s_0,\ldots,s_{m-1}$ is another tagged partition of $[a,b]$ . 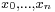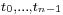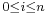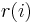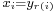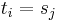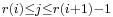We say that $\scriptstyle y_0,\ldots,y_m$ and $\scriptstyle s_0,\ldots,s_{m-1}$ together is a refinement of a tagged partition $\scriptstyle x_0,\ldots,x_n$ together with $\scriptstyle t_0,\ldots,t_{n-1}$ if for each integer $i$ with $\scriptstyle 0 \le i \le n$ , there is an integer $r(i)$ such that $\scriptstyle x_i = y_{r(i)}$ and such that $t_i = s_j$ for some $j$ with $\scriptstyle r(i) \le j \le r(i%2B1)-1$ . Said more simply, a refinement of a tagged partition takes the starting partition and adds more tags, but does not take any away.

References

Gordon, Russell A. (1994). The integrals of Lebesgue, Denjoy, Perron, and Henstock. Graduate Studies in Mathematics, 4. Providence, RI: American Mathematical Society. ISBN 0-8218-3805-9.

Partition of an interval

See also

References